Rolling with Chaos: How Weighted Dice Create Drama in Solo RPGs
Fibonacci Weighting: Rigging Dice Without Cheating
Welcome back everyone, I hope you’ve had an amazing week. Yes, I’m late, and I got a little dramatic about it. Setting goals is important to me, and deadlines bring some of the chaos into to focus. So when I break a deadline, I tend to panic a bit, throw a small fit, and move on.
What else can I do? Sit and dwell on it? No thanks… I’ve got better things to do…
So after lots of running into the wall, just started writing down ideas, and then started asking questions about those ideas. Along the way I discovered Fibonacci Weighted dice rolls.
Please excuse the mess... I threw this together in less than a day.
Dice, Data, and Destiny: How Probability Mirrors the Chaos of Real Life
You’ve rolled dice a thousand times in games. You know a d20 should land on 20 roughly 5% of the time… but when it comes up several times in short period, it feels like the universe is playing with you. Meanwhile, that "50/50" coin toss somehow lands on tails six times straight. What gives?
Turns out, probability isn’t just a game mechanic—it’s the hidden algorithm of reality. And the weird patterns you see in dice? They show up everywhere, from biology to stock markets, often in ways that freak us out.
The Illusion of Patterns (Thanks to our Brain)
Human brains are obsessed with spotting trends, even when they don’t exist. Roll three crits in a row? "This die is lucky!" Flip five tails? "The coin must be weighted!" But statistically, streaks happen—in fact, they’re guaranteed in long enough sequences.
This is called the "clustering illusion"—our tendency to see meaning in random clusters. In reality a coin has a 1 in 64 chance of landing heads six times straight. Unlikely? Sure. Impossible? Not at all.
Studies in psychology (like Gilovich, Vallone & Tversky’s "Hot Hand Fallacy" research) show we wildly misjudge randomness. Basketball fans swear players get "hot streaks," but mathematically, those streaks often match pure chance. Our brains? They make terrible dice.
The Sneaky Power of "Normal Distribution"
Ever graphed 10,000 2d10 rolls? They’ll form a beautiful bell curve—most results cluster near the average (10.5), with extreme highs/lows tapering off. This is the normal distribution, and it’s everywhere.
Above, a heatmap showing the theoretical probability distribution of 10,000 simulated 2d10 rolls. This mathematical model doesn't account for stochastic variables like dice imperfections, rolling surface friction, or human throwing bias which create those unpredictable real-world nuances that live in the gap between calculation and chaos. Nevertheless, the above graph is accurate to a greater extent. What you see above might shift, or even out in the center, but it will always show the variance on the edges; they will almost always be lower than the center values.
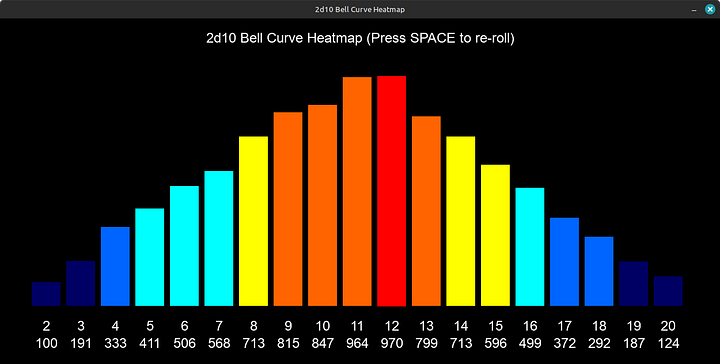
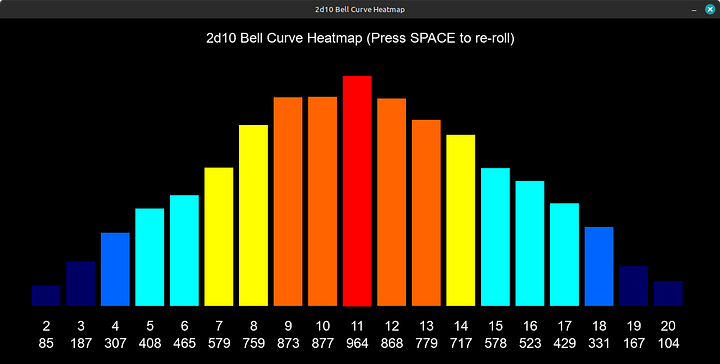
Above, some uncommon, but quite possible variations. In both examples we can see that he left side values showed up more often than the right side values. The opposite can also happen, and so can various extremes of one kind or another; however they only occur in the center, unless some other variable is introduced.
Now, we’re having some fun… Or at least this can lead to fun. The Fibonacci sequence is used to make higher numbers dramatically more likely than lower ones.
Example:
Rolling a 10 is 55 times more likely than rolling a 1.
Rolling a 9 is 34 times more likely than rolling a 1.
...and so on, decreasing down to 1.
This creates a "right-skewed" distribution where high rolls dominate, but rare low rolls still feel shocking, created bias, where we can expect certain results the majority of the time in more specific locations.
Typically you would modify the dice themselves so that they create bias, based on shape, weight in certain areas, and so on. I actually considered this just to test out the results, fortunately there are ways to explore weighted die without physical modification.
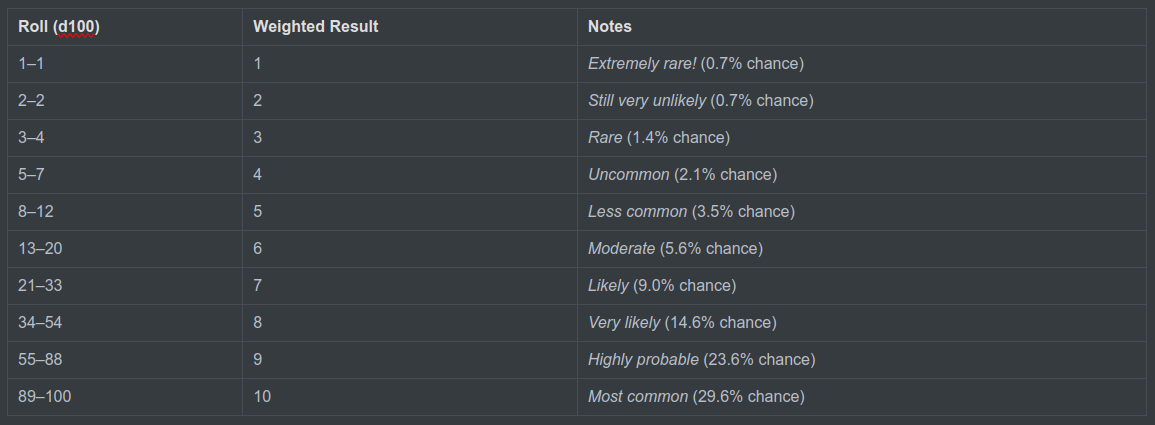
The Fibonacci Weighted d10 Table
Instead of modifying dice, use this lookup table to simulate bias and learn to create your own. Roll a normal d100 (percentile dice) and consult the chart. Here’s what that looks like when we apply that to a dice roll, in this case a 2d10 (aka a d100).
We roll a d100, and the total represents the weighted result. For example, if we rolled a 25, that would result in a weighted result of 7, which falls in the 21-33 range; Likely, with a 14.6% chance of being rolled.
We could easily adjust this by changing the range in which certain numbers are expected to occur in both subtle and extreme ways. We could use this to assure certain actions, emotions, triggers, traps, dungeon types, hair styles, locations in a town… You get the picture.
Let’s say you want to explore a hexmap and want mostly forest type regions.
You do do the same for dungeon contents, encounters, and just about anything else you can imagine.
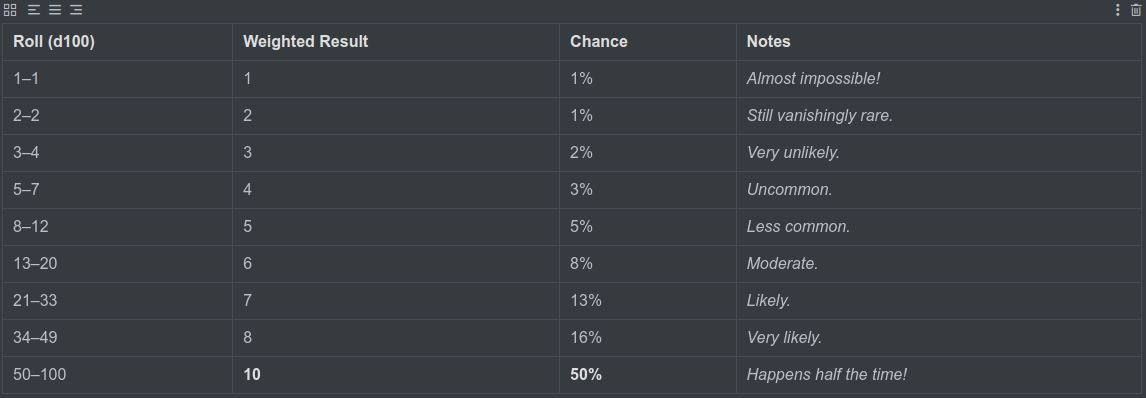
Custom Weighted d10 Table (50% chance for 10)
Roll a d100 and compare:
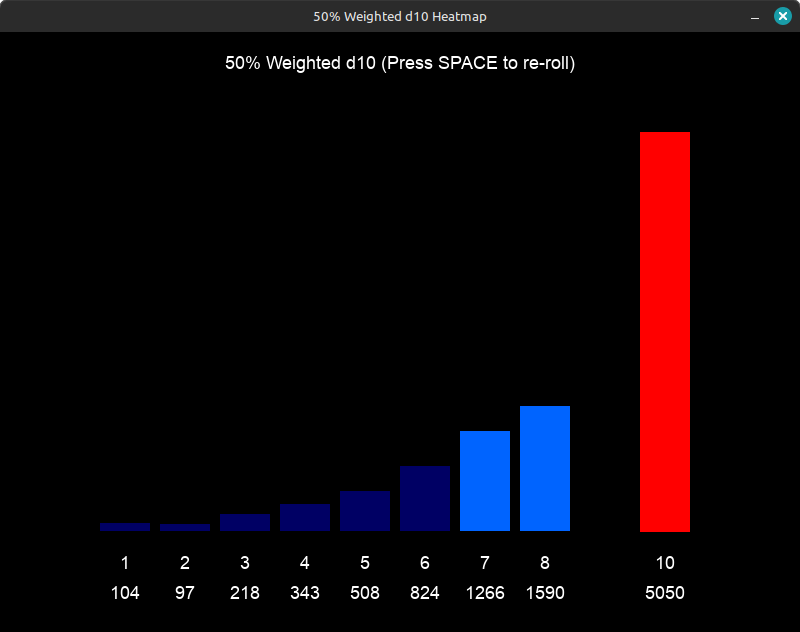
In this case 50% of rolls are likely to result in 10. This puts extreme bias on certain results over others. The distribution of weight can be applied to any area of the table, and isn’t limited to a ten-sided die. You you can easily expand the distribution of values across any number of values and data.
Below is what that would look like:
You can see that out of 10,000 simulated dice rolls, the result of 10, showed up 5050 times. Naturally these numbers shift in occurrence to some degree, but this represents a general outcome.
And yes! I know I left out the chances of rolling a 9, did you not read the caption? Or maybe you don’t get the joke. That’s okay, too.
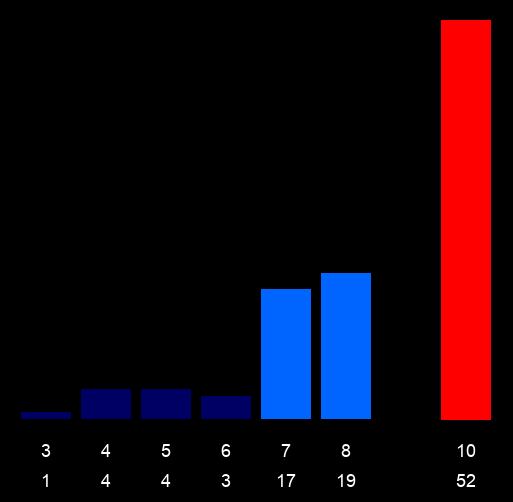
Really, I just I wanted to point out that you can in fact nullify any value or series of data that you don’t want. Why? Well imagine you have a massive wargame going and you don’t want certain enemies to be present until a later time. Let’s say they trigger randomly during the game, for example a roll weighted result of 5. Which is a roll of 8-12 and only 5% chance if we use the 50% weighted heatmap above.
Out of 100 rolls, you could, statistically speaking roll a 5 between once on the low end and up to a possible, but quite uncommon, 13-15 times. In either case, 50% of the time (give or take 2-5%) you’ll be rolling expected results. Filling the table with specific enemies. When a 5 is rolled, you simply skew the results to force a 5 result and flood the table with these unexpected enemies.
Above, we are giving a weighted bias to the value of 5 to represent it being triggered. The number 5 represents a specific type of enemy that was just introduced to the table, and will for a short while at least, be more common than others as they make there way onto the battle field.
Real-world bell curves surround us—heights cluster around averages, with fewer extremes. But stress bends perception like weighted dice. Running late? Suddenly every light’s red. Quantum physics hints reality shifts under observation; particles behave differently when observed, as if the act of looking changes the game.
Now imagine your expectations work the same way. Your brain does the same, amplifying frustrations like a GM fudging rolls against you. The dice aren’t rigged—but your focus is. The universe might not be bending—but your perception is.
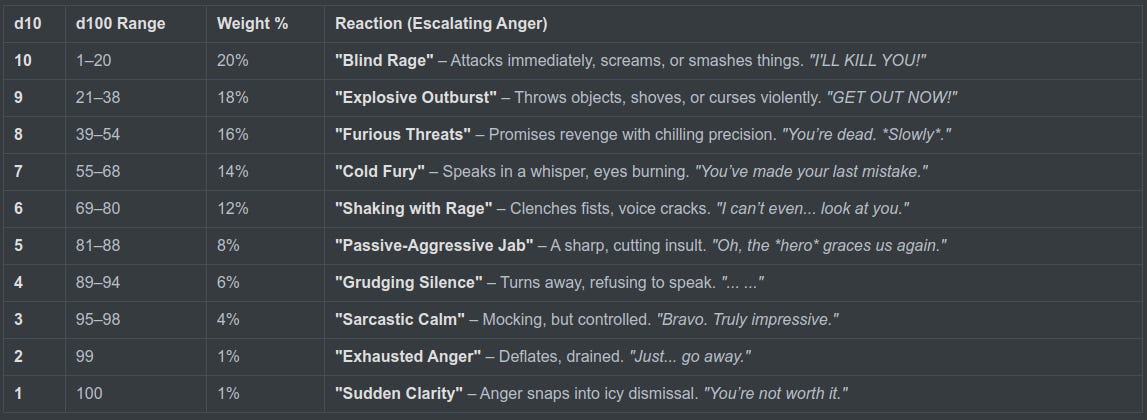
There are some really wide possibilities that can be explored using these methods. For example an angry NPC might have a set number of reactions when they are angry.
You can see how the more serious results are the most common reactions, and the calmer, more self controlled reactions are less common. These are skewed to the extreme for an NPC that really don’t like you much to begin with…
You can feed whatever type of data into a weighted table and tune them to your liking and to suit your own needs. Once you’ve made a few of them you can more easily roll them and decide on the fly what the result is.
Chaos Likes to Dress Up as Patterns
Here’s where it gets eerie. Some "streaks" aren’t random—but spotting the difference is hard:
Pareto Principle (80/20 Rule): In D&D, 20% of your spells likely do 80% of the work. IRL, 20% of people hold 80% of wealth. This isn’t a dice quirk—it’s a power law, common in networks (social media, ecosystems).
"Fat Tails": Financial crashes and pandemics happen way more than normal distribution predicts. Reality has more critical rolls (black swans) than dice do.
Mandelbrot’s fractal math shows nature loves "wild randomness" (earthquakes, stock swings) where extreme events aren’t outliers—they’re baked into the system. Almost hinting at the idea that life and progress thrive on chaos.
A hard lesson to learn, but surely quite obvious if one is being honest.
Modular Threat-Tracking System (MTTS)
Keeping that in mind, here’s a modular threat-tracking system using escalating probability tables to simulate an ancient horror hunting the player through a dungeon. The closer it gets, the higher the chance of a direct encounter.
Threat Level Table (d100)
Roll at the start of each turn to see if the threat advances.
(Adjust ranges to control pacing.)
Note: Once ‘The Horror’ has woken up, 1-50 should be shifted into ‘Awake’—Yes this shifts some responsibility to you the player. And I try not to do that. If it were more complicated then I would break it down into steps, or find a way to automate it. But sometimes you need to put in some work to get the results you want to see. Start small, start now, but start.
And once you’ve started, remember ‘The Horror’ is forever chasing you, so don’t ever stop moving forward.
Distance Table (d20)
When the horror is "Awake" or "Hunting," roll to see how close it gets.
Don’t know the number of rooms? Or are rooms simply abstract ideas? Start with a base value to represents a theoretical distance. For example, 10.
Subtract and add to this value by the number of ‘rooms’ in the Distance Change column. The the closer higher the number gets, the closer the ‘The Horror’. The lower the value, the farther away it is; 20 means it’s right behind you, ‘1’ means it’s way on the other side; probably slacking off. Or maybe it knows about a shortcut…
Modifiers:
+10 if "Hunting" (roll d20+10, cap at 20).
Player actions (e.g., loud noises = +5 to roll).
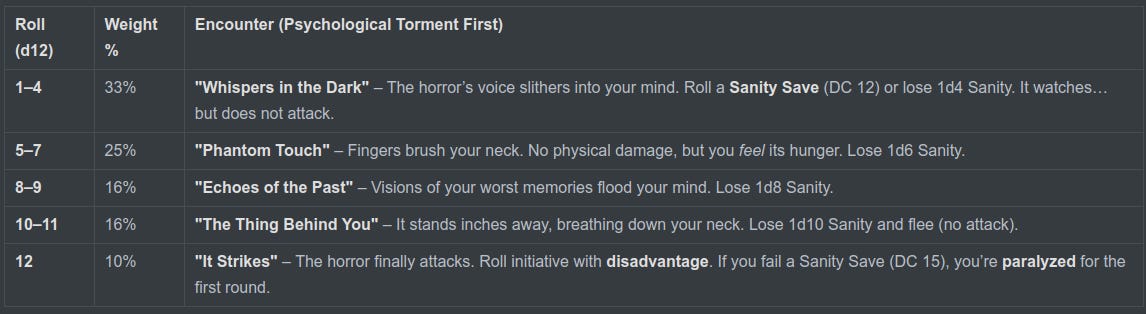
Immediate Encounter Table (d12)
When the horror reaches the player’s room...
Even weight here, but we could easily shift it if say… ‘The Horror’ likes to soak up some of your sanity first.. Then we would add a weight results like we did with the 10 in the early examples. By shifting a good portion of the weight towards certain behaviors. Thereby giving any creature or NPC sense of intelligence and reactiveness in the world.
Sanity-Focused Encounter Table (Weighted d12)
When the horror reaches the player’s room... and wants so play…
Clearly now ‘The Horror’ has a behavior pattern. Imagine how useful that is… That’s also quite expandable don’t you think? What would you apply that to?
Sanity Over Health: 83% of encounters (rolls 1–11) drain Sanity without physical harm. Rare but Deadly Attacks: Only a 12 (10% chance) triggers combat—making it a climactic moment. Escalating Fear: Sanity loss grows (1d4 → 1d10) as the horror closes in.
How to Use It
Sanity Mechanics: Track Sanity like HP. At 0, the player gains permanent madness or flees the dungeon.
Player Choices: Let them spend resources to resist (e.g., "I burn a torch to ward it off—+5 to my Sanity Save").
Tension Curve: Use environmental cues (e.g., "The walls bleed when it’s near") to foreshadow encounters.
Time Escalation (Optional)
Every 3 turns, adjust the Threat Level Table:
Reduce "Dormant" by 10% (e.g., 1–50 → 1–40).
Add 5% to "Upon You" (e.g., 91–100 → 86–100).
And… that is it. For this week on the Solo Roleplaying Buddha. Better late than not at all. I hope you all find this interesting and enjoyable. It’s just a simple walk through of what’s possible with a bit of skewing. Normally weighted results are used for deceitful purposes, but that’s what we want as solitaire players don’t you think? Adding a bit of surprise is essential to creating new paths, new stories, and new adventures.
See you all next week, please take care of yourselves and look out for one another. We’re all we’ve got. Appreciate you.


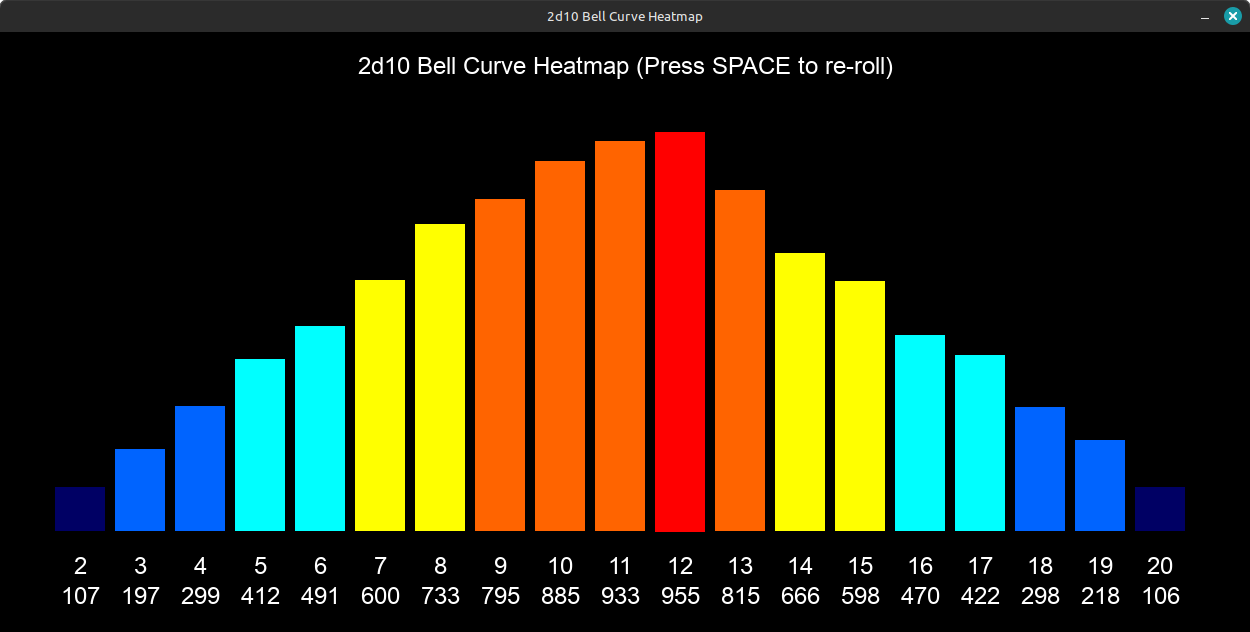
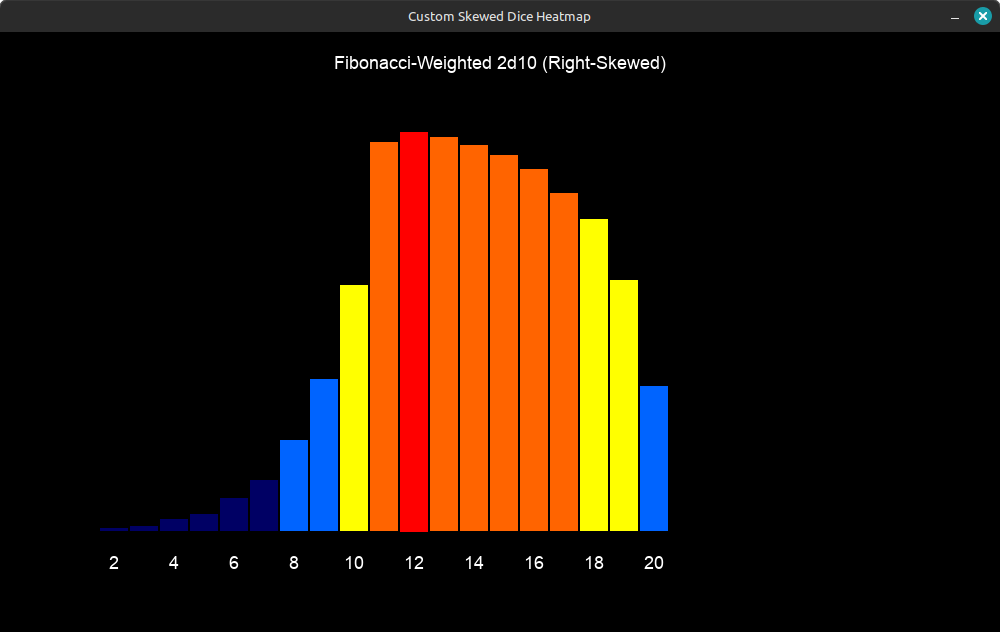





Fascinating.... and brain bending - all at the same time 👍🏻